kap: $k$-Assignment Problem Solver

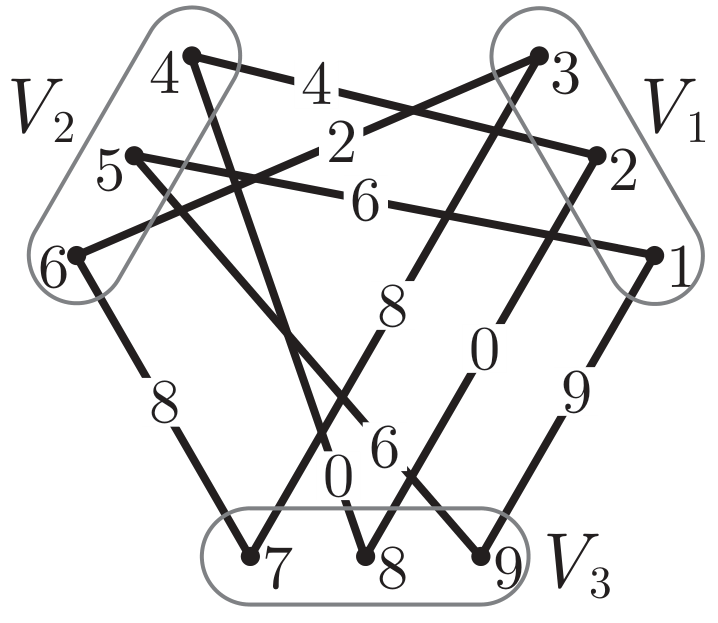
This project implements Boštjan Gabrovšek's Multiple Hungarian Methods for solving the $k$-Assignment Problem (or $k$-Partite Graph Matching Problem), described in this paper.

Background

Problem Formulation

$k$-Assignment (a.k.a. $k$-Partite Graph Matching) Problem is the extension of Linear Assignment (Bipartite Graph Matching) Problem. It is also traditionally referred to as Multidimensional Assignment Problem.

Formally, we seek a $k$-assignment of a given $k$-partite weighted graph $G = (V, E, \omega)$ with the minimum weight:

$$\min{\sum\limits_{\mathcal{Q}}{\omega(\mathcal{Q})\ |\ \mathcal{Q}\text{ is a }k\text{-assignment in }G}}$$

where

$$\omega(\mathcal{Q}) = \sum\limits_{e \in E(G[\mathcal{Q}])}{\omega(e)}$$

This repository provides the implementation of 6 algorithms proposed by Gabrovšek for solving this problem, which is decomposed into small binary sub-problems and tackled with using the Hungarian procedure. While this means we can generalize for an arbitrary number $k$ and use different algorithms other than Hungarian, the methods might not be the most efficient for certain cases (e.g. $k = 3$ a.k.a. the 3-index Assignment Problem).

For more technical details, please refer to the paper or contact the authors, not me 😂.

Context

I implemented this code for testing an idea in another project. After that, I decided to publish the code so that someone facing a similar problem can use. Further maintenance or performance tuning might be limited, but all contribution is welcome.

Requirements

• Python 3.7+
• numpy
• scipy or lap or lapjv or lapsolver or munkres (depends on the backend to be used for solving Linear Assignment Problem)

Installation

Simply run the following command:

pip install kap

Notes

This is currently a pure Python project, but we may add Cython/C++ extension in the future.

Quick Start

Solving Linear Assignment Problem

For convenience, we provide kap.linear_assignment as a wrapper around backend functions. The available backends are:

• scipy: scipy.optimize.linear_sum_assignment's documentation
• lap: https://github.com/gatagat/lap
• lapjv: https://github.com/src-d/lapjv
• lapsolver: https://github.com/cheind/py-lapsolver
• munkres: https://github.com/bmc/munkres

Note that we currently do NOT support sparse matrix. For a benchmark, please head to https://github.com/berhane/LAP-solvers.

The interface is unified as kap.linear_assignment returns a namedtuple of matches, matching_costs of matched edges, and optionally a list of free(or unmatched) vertices if called with return_free=True.

import numpy as np

from kap import linear_assignment

cost = np.array([
    [9, 6, 4],
    [4, 4, 6],
    [3, 9, 2]
])
matching_result = linear_assignment(cost, return_free=True, backend="lap")
print("Result:", matching_result)
# Result: AssignmentResult(matches=array([[0, 2],
#       [1, 1],
#       [2, 0]], dtype=int64), matching_costs=array([4, 4, 3]), free=[])
print("Total cost:", sum(matching_result.matching_costs))
# Total cost: 11

Solving $k$-Assignment Problem

kap.k_assignment is the equivalence for $k$-Assignment Problem. There are a few things to note about its parameters:

• cost_matrices: Sequence of $n (n - 1) / 2$ 2D cost matrices of pairwise matching costs between $n$ partites (might not be able to be represented as a 3D np.ndarray since partites can have different number of vertices) ordered as in itertools.combination(n, 2). For example, $[C_{01}, C_{02}, C_{03}, C_{12}, C_{13}, C_{23}]$.
• algo: This should be one of the six proposed algorithms, namely "Am", "Bm", "Cm", "Dm", "Em", "Fm". $\text{C}_m$ is set to be the default as it usually performs as good as random approaches while having a deterministic behavior.

It's return type shares the same structure as that of kap.linear_assignment but with some small differences:

• matches: Each element is the list of indices of matched vertices. For example, [(0, 0), (1, 1), (2, 0)] indicates that node 0 of partite 0, node 1 of partite 1, and node 0 of partite 3 are matched together. Note that it is NOT necessary for a match to contain at least one vertex from each partite (incomplete graph).
• matching_costs: Each element is the sum of pairwise costs of all edges formed by the matched vertices.

The following code reproduce the example described in the paper.

import numpy as np

from kap import k_assignment

costs = [
    np.array([  # (0, 1)
        [9, 6, 4],
        [4, 4, 6],
        [3, 9, 2]
    ]),
    np.array([  # (0, 2)
        [8, 2, 9],
        [5, 0, 4],
        [8, 7, 4]
    ]),
    np.array([  # (1, 2)
        [4, 0, 9],
        [9, 9, 6],
        [8, 9, 5]
    ]),
]
matching_result = k_assignment(costs, algo="Em", return_free=True, backend="lap")
print("Result:", matching_result)
# Result: AssignmentResult(matches=[[(0, 0), (1, 1), (2, 0)], [(0, 1), (1, 0), (2, 1)], [(0, 2), (1, 2), (2, 2)]], matching_costs=[23, 4, 11], free=[])
print("Total cost:", sum(matching_result.matching_costs))
# Total cost: 38

These code blocks are extracted from examples.

Citation

@software{inspiros_2024_10449791,
  author       = {Hoang-Nhat Tran},
  title        = {inspiros/kap: v0.2.1},
  month        = jan,
  year         = 2024,
  publisher    = {Zenodo},
  version      = {v0.2.1},
  doi          = {10.5281/zenodo.10449791},
  url          = {https://doi.org/10.5281/zenodo.10449791}
}

License

MIT licensed. See LICENSE.txt.