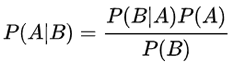本文档是面向程序员秋招的数学基础知识,主要包括简单的数学基础知识以及一些常用的数学公式,并不涉及深入的数学公式推导和证明。内容包括但不限于:概率论与数理统计、线性代数、微积分、离散数学等。如果你想更深入学习数学,可参考更专业的教材
理解贝叶斯公式,首先得了解全概率公式: P(A)=P(A|B1)P(B1) + P(A|B2)P(B2) + ... + P(A|Bi)P(Bi)。
分布律是取某个值的概率,分布函数是积分
- 0-1分布:X ~ B(1, P)
- 二项分布:X ~ B(n, P)
- 几何分布:X ~ G(p) P = (1-p)^k-1 * p
- 泊松分布:描述稀有事件的概率
矩阵的行列式,determinate(简称det),是基于矩阵所包含的行列数据计算得到的一个标量。是为求解线性方程组而引入的。
对角线相乘减去对角线相乘
性质1 行列式与它的转置行列式相等 注:行列式中行与列具有同等的地位,行列式的性质凡是对行成立的对列也同样成立.
性质2 互换行列式的两行(列),行列式变号 推论 如果行列式有两行(列)完全相同,则此行列式为零
性质3 行列式的某一行(列)中所有的元素都乘以同一个倍数k,等于用数k乘以此行列式. 推论 行列式的某一行(列)中所有元素的公因子可以提到行列式符号的外面.
性质4 行列式中如果有两行(列)元素成比例,则此行列式为零.
性质5 若行列式的某一列(行)的元素都是两数之和,则等于对应的两个行列式之和.